Lecture 20

这一节中心思想：计算subgame，然后往前回代。

战争消耗

两位玩家，有两种选择，Fight或者是Quit。

• 要是两者都选择推出，那么本轮的收益为（0, 0），游戏结束。
• 要是一方fight，该方收益V，另一方收益为0。
• 要是两者都选择fight，收益为（-C, -C）。

假设$V>C$

两轮博弈

我们分类讨论，分别讨论纯策略（pure strategy）的结果和混合策略（mixed strategy）的结果。

pure strategy

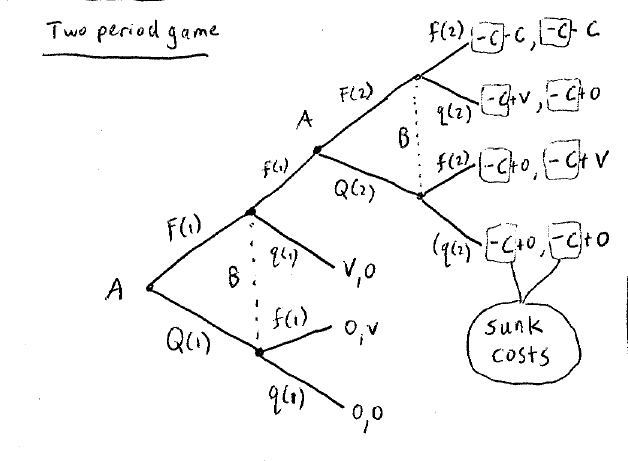
第二轮继续的话，存在前面的沉没成本C。

我们将-C提取出来，并且计算第二轮博弈的NE。

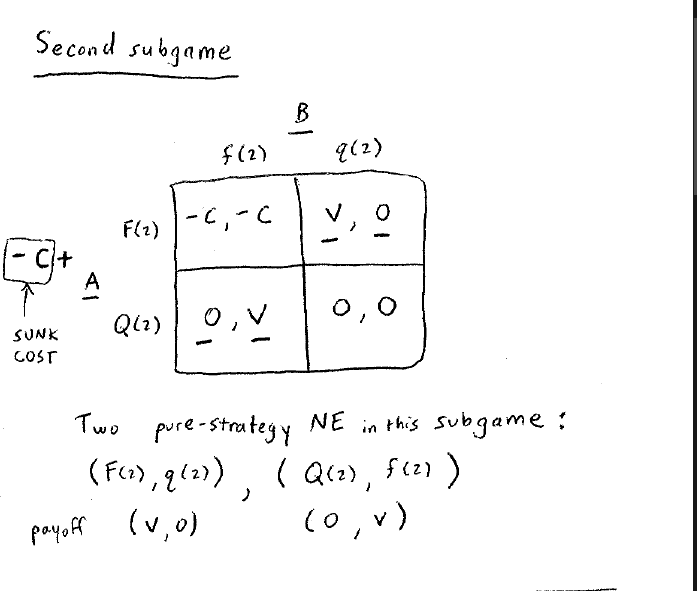
发现有两个NE (F(2), q(2))和(Q(2), f(2))

假设第二局选择的是(F(2), q(2))，那么收益为(v, 0)，在第一轮的博弈中进行回代：

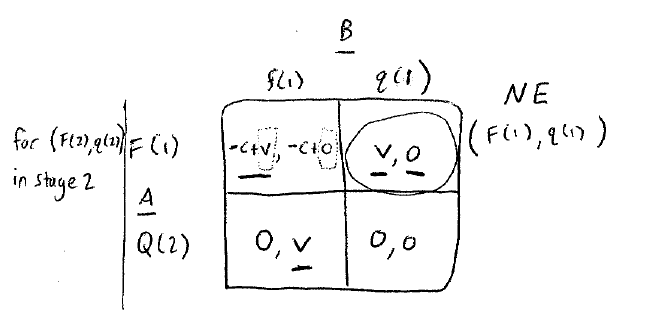
我们发现这个局面的NE为(F(1), q(1))。

同理我们也能第二局选择的是(Q(2), f(2))代入进行计算。

最终，在pure strategy的情况下，有两个纳什均衡点： $[(F(1), F(2)), (q(1), q(2))]\\ [(q(1), q(2)), (f(1), f(2))]$

mixed strategy

我们还是先计算第二轮的NE。

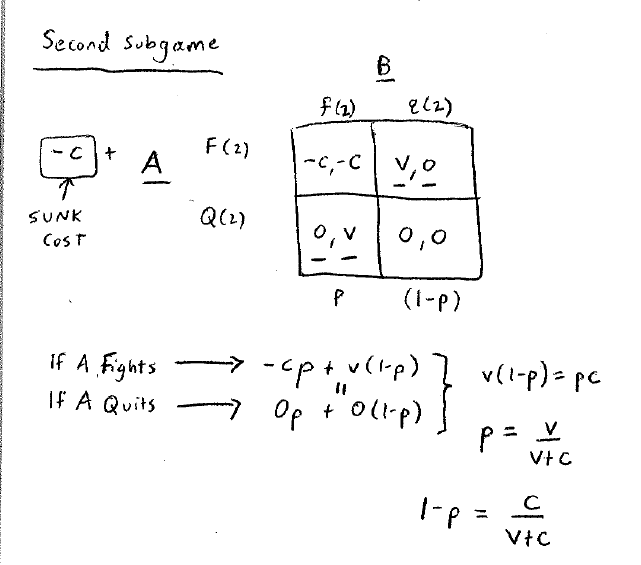
发现在混合策略下，B以$\frac{c}{v+c}$的概率选择fight, 以$1-\frac{c}{v+c}$的概率quit的条件下，A的$payoffs = -cp+v(1-p) = 0*p+0*(1-p) = 0$；同理可以计算B的payoffs = 0。

那么收益为(0, 0)。

带入到第一轮中的游戏中，发现第二轮的游戏与第一轮的游戏一摸一样。

最后得到整体的NE：

$p^* = \frac{v}{v+c}$

$[(p^*, p^*), (p^*, p^*)]$

无限轮

这个就是战争模型了，但是随着博弈次数的增加，两者连续进行战斗的概率指数减小。